Analytical Problem Solving – Ramps

Rocket Car

At time \( t=0 \), the rocket car of mass \( m \) shown below is at location \( s=0 \), with zero speed. At this instant, the parking break is released, and the car begins rolling downhill. The hill is at an angle \( \theta \) relative to horizontal as shown. At time \( t = t_a \), the driver turns on the rocket which immediately produces a constant thrust \( F_T \).

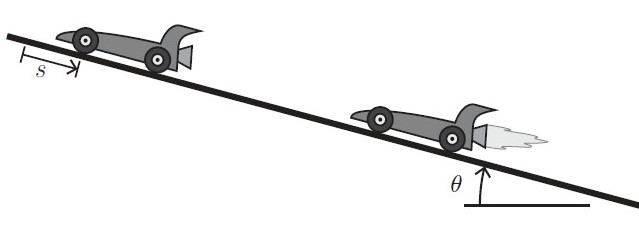
Assume that the thrust produced by the rocket is sufficiently large that the car eventually travels back uphill and passes the original starting point. Given \( m \), \( \theta \), \( F_T \), \( t_a \), and gravitational field strength \( g \), find the following. (1) The time, \( t_d \), it takes for the car to switch directions and start heading back uphill; (2) the distance, \( d \) the car travels downhill before turning around.

You can find a qualitative/graphical solution to this problem here. An analytical problem-solving solution is provided below.