Review of Calculus Principles

In order to understand dynamics, you are going to have to understand basic principles of integral and derivative calculus. For this reason, I have posted some notes on derivatives and integrals. When you understand the principles, you should be able to complete the practice problems I have included.

An Intuitive Example Problem: Water Tank

Here is a thought exercise that intuitively reveals the relationship between derivative and integral. Download the PDF here, then try it on your own. When you think you have something, come back and check your answer.

Important take-aways from this problem

The net flow rate, $ Q $, and the tank volume, $ V $ are related by a derivative:

$$ \frac{dV}{dt} = Q. $$

To put this in simple words, we could say:

The rate of change of the volume of water, $V $, in the tank is equal to net flow rate, $Q $, of water into the tank.
Whenever the the net flow rate into the tank, $Q$, is positive, then the volume, $V$ should be increasing.
Whenever the the net flow rate into the tank, $Q$, is negative, then the volume, $V$ should be decreasing.

We can also think of the two quantities as being related by a definite integral:

$$ V(t_2) – V(t_1) = \int_{t_1}^{t_2} Q(t) dt.$$

To put this in words, we would say:

The change in volume between times $t_1$ and $t_2$ is equal to the area under the $Q$ curve between these times.
If there is net positive area under the $Q$ curve, then there is a net increase in volume, $V$, over this time interval.
If there is net negative area under the $Q$ curve, then there is a net decrease in volume, $V$, over this time interval.

Calculus Reference Material

I’m going to offer you two different ways to review concepts of differentiation and integration. The first is a document that I wrote a few years ago. The second is a series of beautiful videos created by Grant Sanderson (3 Blue 1 Brown). You may choose either of these approaches, or both.

The Document

This document discusses how to think about the derivative and integral, based on the definitions of the operations. I have created video versions of parts of the calculus review in case you prefer to listen/watch the material, rather than read: Definition of Derivative; Check Your Understanding of Derivative; Check Your Understanding of Integral.

The Videos

Here are those gorgeous videos I mentioned. By illustrating how one would calculate the area of a circle using calculus-like thinking, Sanderson elegantly illustrates the Fundamental theorem of calculus.

In this second video, he illustrates the derivative by thinking about the “velocity” of a car. I do the same in my notes, but Sanderson’s is so much more beautiful. I just have two small beefs with the video. First, he uses the word “velocity” when he should say “speed.” Secondly, I disagree with the paradox he talks about. There’s nothing inconsistent about a moving object having zero velocity (motionless) for just an instant. If you want, you can stop watching after time 10:25.

And finally, a video on integration and its relationship with the derivative (i.e. the Fundamental theorem of calculus).

Take-Aways, Derivative

A time derivative is a measure of how fast something is changing at some instant.
If we have a plot of some function with respect to the dependent variable t, then the derivative of the function with respect to t, evaluated at t=t0, is the slope of the tangent line at t=t0.
If something is increasing with respect to time, then its time derivative is positive.
If something is decreasing with respect to time, then its time derivative is negative.
When something is NOT changing, even for an instant, its time derivative must be zero at that instant.

Take-Aways, Integral

One can think of an integral as the opposite of derivative, an “anti-derivative.”
One can think of an integral as a signed area under the curve.
When the integrand (function you’re integrating) is positive, the integral of that function should be increasing.
When the integrand is negative, the integral of that function should be decreasing.
When the integrand is zero, the integral should not change, at least for a brief moment.
For indefinite integrals, there is an arbitrary constant of integration.

Check Your Understanding, Derivative

To check your understanding of the derivative, I would like you to consider the plot below which shows a function x of a variable t. Given your understanding of the derivative, could you sketch (by hand) a plot of the derivative of function x with respect to t? Think about it. Try it!

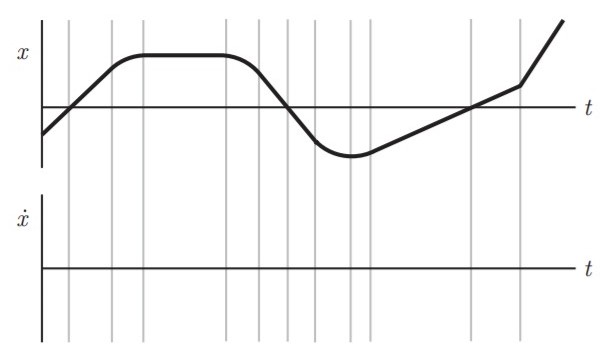
To check your results, see the video here.

Check Your Understanding, Integral

Now consider the function in the figure below. This time I want you to sketch a plot of the integral of the function. You can set the initial condition at t=0 to zero if you wish. Think about it. Try it!

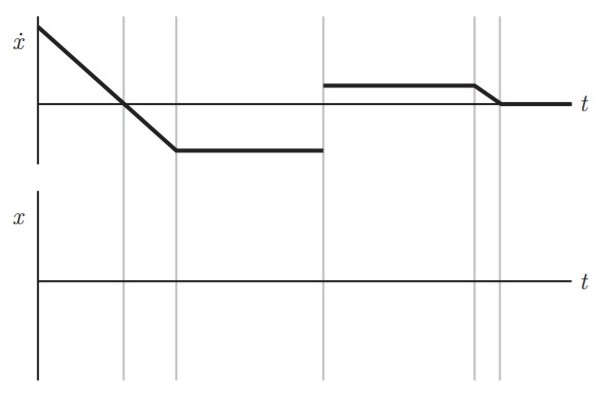
To check your results, see the video here.

Practice Problems

To help you understand differentiation and integration at a level that will help you understand dynamics, you should try answering these four practice problems.

Answers to Practice Problems

After you work out the practice problems you should check your answers. I have answers posted in two formats below. The PDFs are there if you want a quick look at the answers. I have also posted videos in case you want to hear my explanation.

Video for Problem A:

Video for Problem B:

Video for Problem C:

Video for Problem D: