Review of Vectors

 

In order to understand dynamics, you are going to have to think naturally in terms of vectors. Speaking and thinking in terms of vectors should be as easy as speaking in your native language. In effort to refresh your memory, I have posted some material and problems that I would like you to work through.

List of Topics

Vector Addition, Scalar Multiplication, and Basis Vectors

The notes that I wrote on this topic several years ago are provided at the bottom of this page. Since then, Grant Sanderson (3 Blue 1 Brown) made some video that describe and illustrate the material much better. Therefore, I’m going to ask that you watch them.

This first video explains what a vector is, along with the meaning of vector addition and scalar multiplication. Please give it all your attention.

This next video introduces the idea of basis vectors, and how the same vector can have different representations with different choices of basis vectors. At about 4:15 into the video, it starts talking about “span.” Span is an important concept in many fields of study, but it’s not particularly important in engineering dynamics, so you may stop at 4:15 if you choose. But it certainly wouldn’t hurt to watch the video to the end.

Vector Subtraction

In the previous section, we saw that to add to vectors \(\underset{\sim}{\boldsymbol{A}}\) and \(\underset{\sim}{\boldsymbol{B}}\), we arrage the vectors tip-to-tail as shown below.

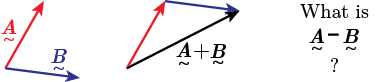
Graphical representation of vector subtraction.

The question now is, what does the vector \(\underset{\sim}{\boldsymbol{A}}- \underset{\sim}{\boldsymbol{B}}\) look like? Think about this for a while. Can you derive the result from the definition of vector addition. Once you have an answer, watch the video below.

Vector Decomposition

Here’s the basic idea.

Recipe for Decomposition

  1. Draw a vector triangle. (a) Two sides of the vector triangle should be tangent to the basis vectors (e.g. \(\hat \imath\) and \(\hat \jmath\)). Those two component vectors, when placed tip to tail, should add up to the original vector, which is the hypotenuse of the right triangle. Make sure the arrows on the triangle conform to the rules of vector addition.
  2. Identify a key angle (or side ratio). In the original problem, there is an angle or side ratio that defines the orientation of the vector to the basis vectors. You need to identify that angle in the force triangle.
  3. Use trigonometric principles to calculate magnitudes of the component vectors. Many students use mnemonics (e.g. SOH-CAH-TOA) to remember to remember definitions of trigonometric functions. Now that you’re an engineer, it’s time to lose the crutch. Commit the definitions to memory.
  4. Write the original vector in terms of its components. Be sure to get the signs of the components right. If a component vector is in the opposite direction of the corresponding basis vector, then the component must be negative.
  5. Check that your answer makes sense.

Using the checklist on force vectors of a free body diagram.


Now we’ll decompose the same forces, but with different basis vectors.

Decomposition Practice Problems: You will find them here.

Notes

PDF logo. Link to vector notes.Here is an incomplete set of notes that provide a refresher for thinking about and working with vectors.

For the vector decomposition portion of the notes, there is a two-part video: Video Part 1, Video Part 2.