Introduction to Analysis Without Equations
List of Links
Why Analyze Without Equations?
One of the traps that engineering students often fall into is that they think of dynamics problem-solving as an exercise in trying to find the “right equation.” They hunt through textbooks and course notes to find mathematical expressions that relate given quantities to other quantities they want to calculate. To students, dynamics knowledge can be summarized as a set of symbols on an equation cheat sheet that they might be able to bring to an exam.
Experts, on the other hand, see meaning in the equations. They see a description of how the mechanical world works. They see connections between the concepts; they see a story of how one principle follows from another. When it comes to solving problems, mathematical equations are often the most efficient way of expressing and communicating ideas, as well as quantifying the consequences of those ideas. But it’s the physical principles expressed by the equations that are central to the problem solving process, not the equations themselves.
In this page, I pose a few engineering analysis problems that ask for a qualitative answers rather than a quantitative ones. Not seeing anything to calculate, students often abandon use of the equations and all the physical ideas contained in the equations. They switch to their gut instincts and intuition in solving the problem rather than a systematic application of physical principles.
Here we work on solving qualitative mechanics problems. As always in this course, the problems have to be answered and justified rigorously. In your analysis of these problems, you are not allowed to solve equations or manipulate the symbols in equations. Gut instinct and intuition is not permitted either. Instead, you must solve the problems and justify your answers by invoking the physical principles verbally and/or diagrammatically.
Two Frame Problems from Statics
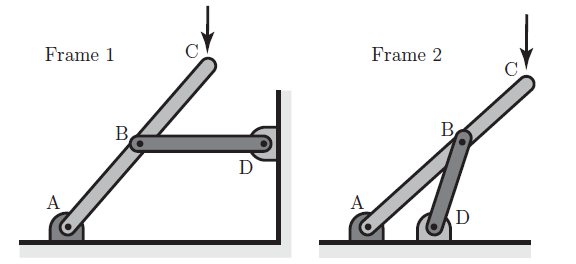
The figure below shows two frames. Each is loaded with a downward force at point C. Each is in static equilibrium. Points A, B, and D for each frame are pin joints. Assume that the weight of the frames are negligible compared to the applied loads.
For each of the two frames, determine the general direction of the forces at point A acting on the frames. Your choices are: directly upward, directly downward, directly to the left, directly to the right, upward and to the left, upward and to the right, and downward and to the left, downward and to the right.
Justify your answers with a rigorous “Analysis without Equations”, based on physical principles of equilibrium that you learned in statics.
Solutions
Written solution will be provided soon. Video solutions are provided below.
Frame 1
Frame 2
Truss Problem from Statics
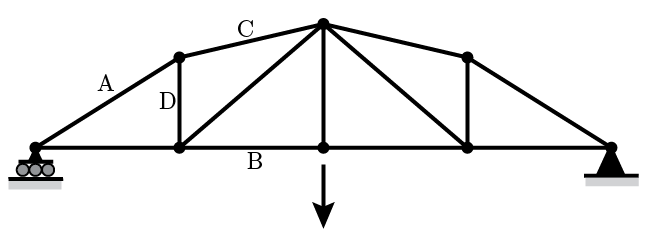
Here is another statics problem that you can do for practice.
Consider the truss shown above, with a load attached to the middle. Perform an “Analysis without Equations” to answer the following questions. You may want to do something similar to the method of joints or method of sections, or both, but without equations.
- Is member A in compression or tension?
- Is member B in compression or tension?
- Is member C in compression or tension?
- Is member D in compression or tension?
- Which member is carrying more load, member A or C?