Impulse-Momentum Principle (Linear)
On this page, we discuss the Impulse-Momentum Principle. Right now we work on the LINEAR momentum version of the principle. It’s a framework that’s particularly powerful for studying problems involving collisions. We start with the theory and then go on to work through a few practice problems.
Table of Links
- Theoretical Background
- Collisions and Energy (Coming Soon)
- Coefficient of Restitution Part 1
- Coefficient of Restitution Part 2
- Practice Problem A
- Practice Problem B
- A Concept Problem
Theoretical Background
Here we derive the impulse momentum principle, directly from Newton’s Second Law. Then we show why it’s so useful when studying collections or systems of particles. In particular, the impulse-momentum principle allows one to eliminate effects of internal forces (i.e. forces between particles within the system).
Coefficient of Restitution, Part 1
The coefficient of restitution provides a measure of how “springy” objects are when they collide into each other. In the Part 1 video, we introduce why the coefficient of restitution is useful, and develop it for the simple case of an object colliding with an immovable body.
Coefficient of Restitution, Part 2
Here, we build on the previous video and develop the coefficient of restitution for a central impact problem in which masses move along a straight line.
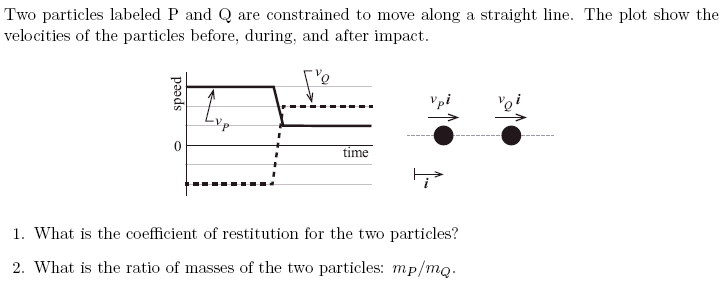
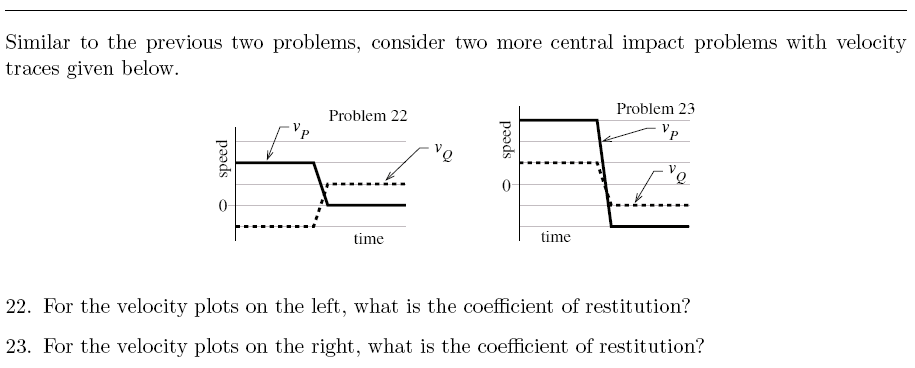
Practice Problem A
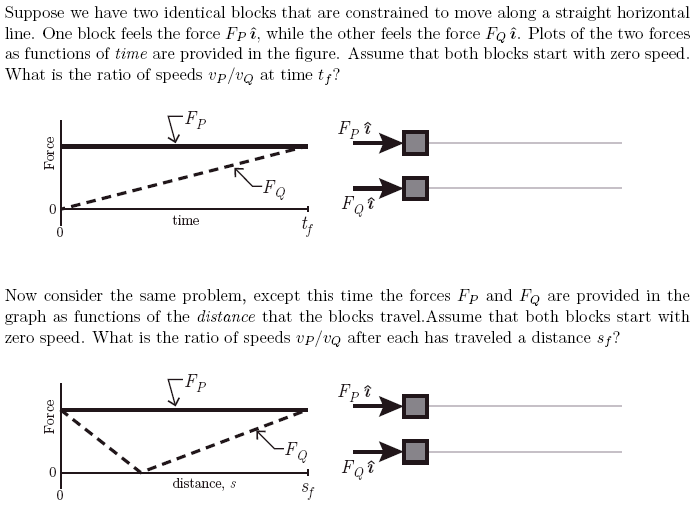
Practice Problem B
Answers are in the following video.
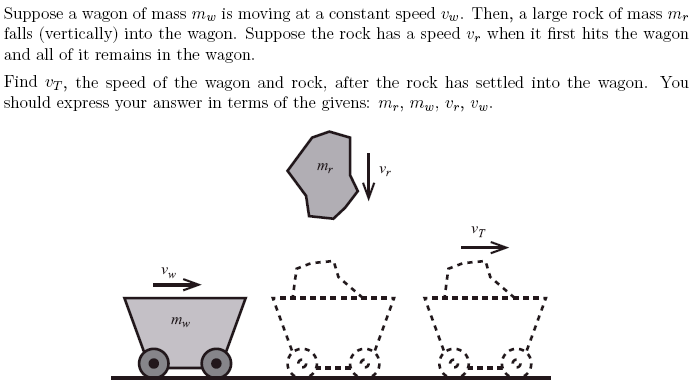
A Concept Problem
The following problem tests whether you understand important concepts discussed on this page and perhaps other pages as well.
Answers